Euler Yet another proof Engine - EYE
EYE is a reasoning engine supporting the Semantic Web layers.
It performs forward and backward chaining along Euler paths.
Via N3 it is interoperable with Cwm.
Forward chaining is applied for rules using => in N3 and backward chaining
is applied for rules using <= in N3 which one can imagine as built-ins.
Euler paths are roughly "don't step in your own steps" which is inspired by
what Leonhard Euler discovered in 1736 for the Königsberg Bridge Problem.
EYE sees the rule P => C as P & ˜C => C.
Architecture and design
The EYE stack comprises the following Software and Machines:
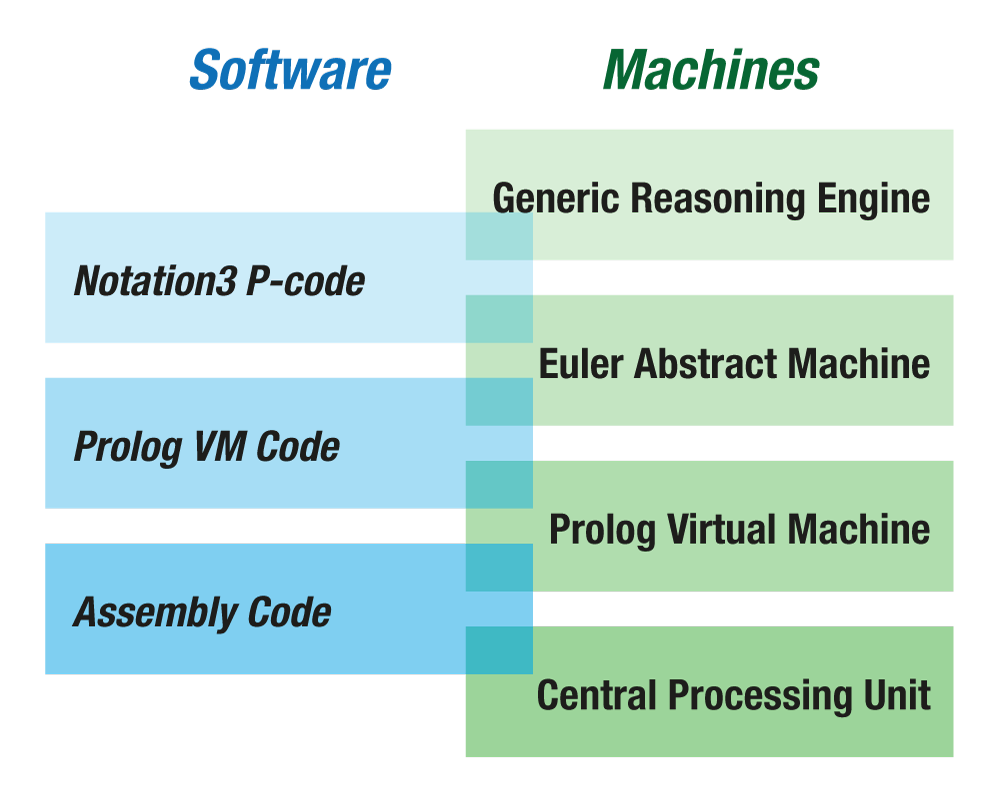
This is what the basic EAM (Euler Abstract Machine) does in a nutshell:
- Select rule
P => C
- Prove
P & ˜C (backward chaining) and if it fails backtrack to 1.
- If
P & ˜C assert C (forward chaining) and remove brake
- If
C = answer(A) and tactic limited-answer stop, else backtrack to 2.
- If brake or tactic linear-select stop, else start again at 1.
Unifying Logic
Explainable Reasoning
Running the Semantic Web Databus and Proofbus from Tim Berners-Lee which is
like a world wide welding machine transforming data into proofs:
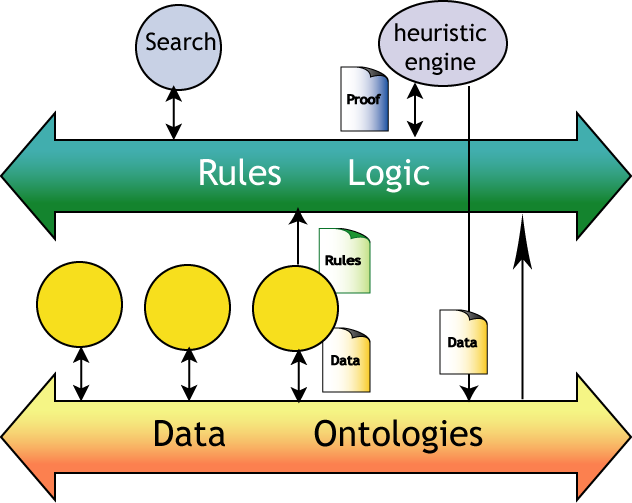
For EYE we strive to realize the inherent potential of mathematical reasoning:
- direct proof: a logical method starting from the statement to be proven (top-down) and known facts or axioms
(bottom-up), working step-by-step from both directions until they meet to form a complete logical argument.
- proof by contrapositive: a logical method where you prove that if the conclusion is false, the premise must
also be false, which is logically equivalent to proving the original statement.
- proof by contradiction: a logical method where you assume the negation of the statement to be proven,
derive a contradiction, and conclude that the original statement must be true.
- proof by cases: a logical method where a statement is proven by dividing it into distinct, exhaustive cases
and demonstrating that the statement holds true in each case.
- proof by recursion: a logical method of establishing a result by defining a base case and a recursive step
that derives the solution for larger cases from smaller ones.
EYE reasoning assumptions
- N3 rules can only have quickvars and they have rule scope
- Quickvars are interpreted universally except for forward rule conclusion-only variables which are interpreted existentially
- Blank nodes are interpreted existentially and have document scope
Examples and Test Cases
- bayesian networks:
ccd,
nbbn,
swet
- control systems:
acp,
cs
- description logic:
bmt,
dt,
edt,
entail,
gedcom,
h2o,
RDF plus OWL
(source)
- ershovian compilation:
preduction
- extensible imaging:
lldm
- graph computation:
graph,
path-discovery
- logic programming:
4color,
dp,
diamond-property,
gcc,
hanoi,
lee,
n-queens,
socrates,
witch,
zebra
- markovian networks:
mmln
- mathematical reasoning:
ackermann,
eulers-identity,
fibonacci,
padovan,
peano,
peasant-multiplication,
peasant-power,
pi,
polygon,
tak
- neural networks:
fcm,
fgcm
- quantum computation:
dqc
- universal machines:
turing,
usm
- workflow composers:
gps,
map,
resto,
restpath,
twf
See also